conic section

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U shaped. It fits several other superficially different mathematicaldescriptions, which can all be proved to define exactly the same curves.

Part of a parabola (blue), with various features (other colours). The complete parabola has no endpoints. In this orientation, it extends infinitely to the left, right, and upward.

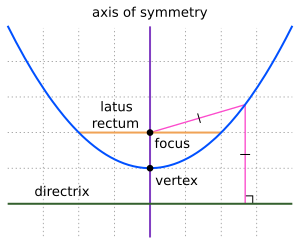
One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane which is parallel to another plane that is tangential to the conical surface.^[a]

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola).

Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is:

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.}$

Assuming a ≥ b, the foci are (±c, 0) for ${\displaystyle c={\sqrt {a^{2}-b^{2}}}}$. The standard parametric equation is:

${\displaystyle (x,y)=(a\cos(t),b\sin(t))\quad {\text{for}}\quad 0\leq t\leq 2\pi .}$

Ellipses are the closed type of conic section: a plane curve tracing the intersection of a cone with a plane (see figure). Ellipses have many similarities with the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded. An angled cross section of a cylinder is also an ellipse.

An ellipse may also be defined in terms of one focus point and a line outside the ellipse called the directrix: for all points on the ellipse, the ratio between the distance to the focus and the distance to the directrix is a constant. This constant ratio is the above-mentioned eccentricity ${\displaystyle e={\tfrac {c}{a}}={\sqrt {1-{\tfrac {b^{2}}{a^{2}}}}}}$.

===============================================================================

NOW IF YOU ARE SOLVING 

BEST REVISION BOOK OF MATHEMATICS BY ER. SHAMBHU KUMAR BELOW LINK MAY BE USEFUL TO YOU.
jee main 2013-2018 Questions:


Jee main 2013-2018 Solutions(part 1):

jee main 2013-2018 Solutions(part 2):

jee main 2019 Questions: